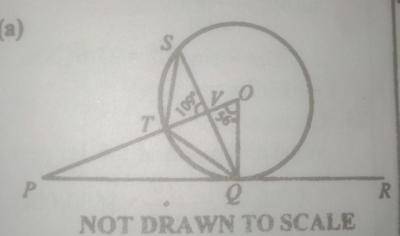
(a) In the diagram above, \(\overline{PR}\) is a tangent to the circle O at Q. \(\angle\)POQ = 56º and  \(\overline{PO}\) intersect  \(\overline{SO}\) at V such that \(\angle\)SVP = 109º. Calculate: (i) \(\angle\)TQP (ii) \(\angle\)QTS

(b) Simplify \(\frac{2n^2 - 3n - 2 }{2n^2 + 3n + 1} \times \frac{n^2 - 1}{n^2 - 4}\)

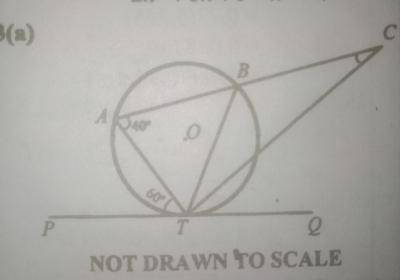
(a) In the diagram above, ABT is a circle centre O. \(\overline{PQ}\) is a tangent to the circle at T and ABC is a straight line. \(\overline{TC}\) bisects \(\angle\)BTQ, \(\angle\)BAT = 44º and \(\angle\)PTA = 60º. Find \(\angle\)ACT

(b) The circumference of the base of a cylindrical tank is 11 m. The height of the tank is 3 m more than 6 times the base radius. Calculate the:

(i) radius; (ii) height; (iii) volume of the tank.

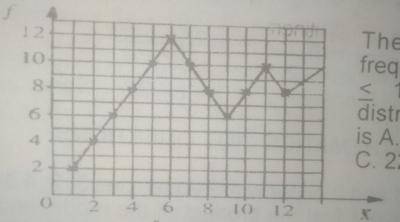
The cumulative frequency for 5\(\leq\) x \(\leq\) 12 from the distribution above is 

Evaluate \(\begin{pmatrix}3 & -2 \\-7 & 5 \end{pmatrix}\) + 2\(\begin{pmatrix}-2 & 4\\3 & -1 \end{pmatrix}\)

If f(x) = 3x - 2I, P = \(\begin{pmatrix}2 & 1 \\-1 & 0 \end{pmatrix}\) and I is 2 x 2 identity matrix. Evaluate f(p)