(a) Copy and complete the table of values for the relation y = 3 sin 2x.
| x | o\(^o\) | 15\(^o\) | 30\(^o\) | 45\(^o\) | 60\(^o\) | 75\(^o\) | 90\(^o\) | 105\(^o\) | 120\(^o\) | 135\(^o\) |
\(^o\) |
| y | 0.0 | 1.5 | -2.6 |
(b) Using a scale of 2 cm to 15° on the x-axis and 2cm to I unit on the y-axis, draw the graph of y = 3 sin 2x for 0° \(\geq\) x \(\geq\) 150°.
(c) Use the graph to find the truth set of;
(i) 3 sin 2x + 2 = 0;
(ii ) \(\frac{3}{2}\) sin 2x = 0.25.
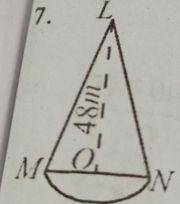
(a) The diagram shows a wooden structure in the form of a cone, mounted on a hemispherical base. The vertical height of the cone is 48 m and the base radius is 14. Calculate, correct to three significant figures, the surface area of the structure, [Take \(\pi = \frac{22}{7}\)]
(b) Five years ago, Musah was twice as old as Sesay. If the sum of their ages is 100, find Sesay's present age.
(a) Ms. Maureen spent \(\frac{1}{4}\) of her monthly income at a shopping mall, \(\frac{1}{3}\) at an open market and \(\frac{2}{5}\) of the remaining amount at a Mechanic workshop. If she had N222,000.00 left, find:
(i) her monthly income.
(ii) the amount spent at the open market.
(b) The third term of an Arithmetic Progression (A. P.) is 4m - 2n. If the ninth term of the progression is 2m - 8n. find the common difference in terms of m and n.
(a) Two cyclists X and Y leave town Q at the same time. Cyclist X travels at the rate of 5 km/h on a bearing of 049° and cyclist Y travels at the rate of 9 km/h on a bearing of 319°.
(a) Illustrate the information on a diagram.
(b) After travelling for two hours, calculate. correct to the nearest whole number, the:
(i) distance between cyclist X and Y;
(ii) bearing of cyclist X from Y.
(c) Find the average speed at which cyclist X will get to Y in 4 hours.
The table shows the distribution of marks obtained by students in an examination.
| Marks (%) | 0 - 9 | 10 - 19 | 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | 60 - 69 | 70 - 79 | 80 - 89 | 90 - 99 |
| Frequency | 7 | 11 | 17 | 20 | 29 | 34 | 30 | 25 | 21 | 6 |
(a) Construct a cumulative frequency table for the distribution.
(b) Draw the cumulative frequency curve for the distribution.
(c) Using the curve, find correct to one decimal place, the:
(i) median mark;
(ii) lowest mark for the distinction if 5% of the students passed with distinction