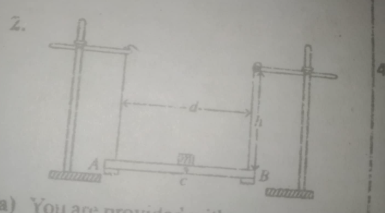
(a) You are provided with two metre rules, two retort stands, a mass, m = 100g, thread, and other necessary apparatus
(i) Place one of the metre rules on a knife edge and determine the centre of gravity, C
(ii) Measure and record the mass, M\(_R\) of the metre rule
(iii) Attach the mass = 100g firmly to the metre rule AB at C using paper tape
(iv) Suspend the metre rule by two parallel threads of length, h = 40cm each at 10 cm and 90cm mark. Ensure that the graduated face of the metre rule is facing upwards.
(v) Set the metre rule into small angular oscillation about the vertical axis through the centre of gravity.
(vi) Determine the time, t for 20 complete oscillations. Evaluate the period T and T\(^2\).
(vii) Read and record the value of d in metres.
(viii) Keeping d, constant, repeat the procedure for four other values of h = 50, 60, 70, and 80 cm. In each case, determine t and evaluate T and T\(^2\).
(ix) Tabulate the readings
(x) Plot a graph of T\(^2\) on the vertical axis and h on the horizontal.
(xi) Determine the slope, s of the graph
(xii) Evaluate K = \(\frac{\text{S}}{\text{Q}}\) where Q = \(\frac{2}{25d^2}\)
(xiii) State two precautions taken to ensure accurate results
b(i) Define couple as it relates to oscillatory motion
(ii) Give two practical applications of a couple in everyday life.
(a)i c = 50.0cm
(ii) M\(_R\) = 90.0 g
(vii) d = 0.8m
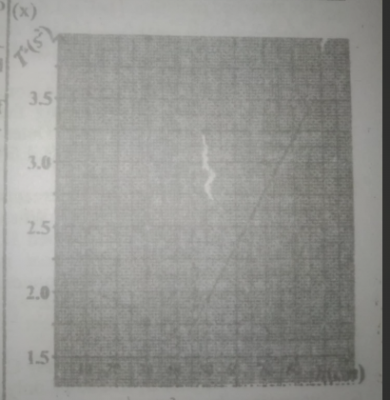
(ix)
| S/N | h(cm) | t(s) | T= \(\frac{t}{20}\)s |
T\(^2\)s\(^2\) |
| 1 | 40.0 | 26.12 | 1.306 | 1.7056 |
| 2 | 50.0 | 27.80 | 1.390 | 1.9321 |
| 3 | 60.0 | 30.68 | 1.534 | 2.3532 |
| 4 | 70.0 | 34.60 | 1.730 | 2.9929 |
| 5 | 80.0 | 35.80 | 1.790 | 3.2041 |
(x) SEE THE GRAPH ABOVE
(xi) Slope, s = \(\frac{ΔT^2}{Δ h}\) = \(\frac{3.0 - 1.75}{75 - 46}\) = \(\frac{1.25}{29}\) = 0.431s\(^2\)cm\(^{-1}\)
(xii) K = \(\frac{\text{S}}{\text{Q}}\)
where, Q = \(\frac{2}{25d^2}\) = \(\frac{2}{25 \times (0.8)^2}\) = 0.125
K = \(\frac{\text{S}}{\text{Q}}\) = \(\frac{0.431}{0.125}\) = 0.3448
b(i) A couple, as related to oscillatory motion, refers to a pair of forces that are equal in magnitude but opposite in direction, and act on opposite sides of a pivot or fulcrum, causing rotation or torsion.
b(ii) I. Wrenches: When using a wrench to tighten or loosen a bolt, the force applied creates a couple that produces rotational motion. II. Steering Wheels: Turning the steering wheel of a car applies a couple that rotates the front wheels, allowing for directional change. III. Door Handles: When pushing or pulling on one side of a door handle, a couple is created that rotates the door about its hinges. IV. Bicycle Pedals: When pedaling a bicycle, the force applied to the pedals generates a couple that turns the crankshaft, propelling the bike forward.
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}