PART2
(a) State the effect of increasing temperature on the viscosity of a: (i) liquid, (ii) gas
(b) State two factors that determine the magnitude of a moment of a force
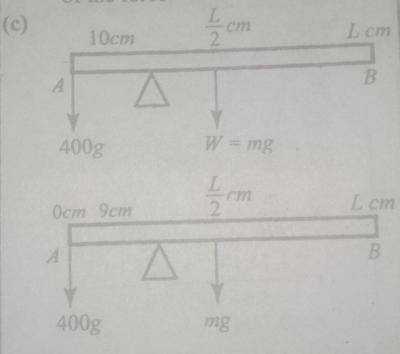
(c) A uniform stick AB of length, L, and mass, m, is balanced horizontally on a knife edge 10.0cm from A when an object of 400 g is suspended at A. When the knife edge is moved 5 cm further, the object has to be moved to a point 9.00 cm from A for the stick to balance.
(i) Represent the balance system with a suitable diagram
(ii) Determine the: I. mass, m of the stick; II. length, L.
(d) Explain in terms of air molecules why pressure at the top of a high mountain is less than at sea level.
(e) Mercury of density 13.6 x 10\(^3\)kgm\(^{-3}\) is poured in a container of uniform cross-sectional area 40cm \(^2\) to a height of 20 cm. The total pressure exerted on the base of the container is 1.42 x 10\(^5\)P. Calculate the: (i) mass of the mercury in the container and (ii) pressure exerted at the surface of the mercury. [g = 10ms\(^{-2}\)
(ai) Increasing the temperature of a liquid decreases the viscosity of the liquid. (aii) Increasing the temperature of a gas increases the viscosity of the gas
(b) Factors that determine the magnitude of the moment of a force about a point are: 1. Angle between the distance from the turning point and the line of action of the force. 2. magnitude of the applied force. 3. perpendicular distance from the pivot to the line of action of the applied force.
(c) SEE THE DIAGRAM ABOVE.
(ii) Taking a moment about the support: clockwise moment = anti-clockwise moment
400 x 10 = m x (\(\frac{L}{2}\) - 10) -- ------- from figure 1 above
4000 = m x (\(\frac{L}{2}\) - 10) - - - -- - - (i)
400 x 6 = m x (\(\frac{L}{2}\) - 15) - - - - -- - - -(ii)
divide eqn i by ii
\(\frac{4000}{2400}\) = \(\frac{m \times \frac{L}{2} - 10)}{m \times \frac{L}{2} - 15)}\)
\(\frac{5}{3}\) = \(\frac{\frac{L}{2} - 10)}{\frac{L}{2} - 15)}\)
3 x (\(\frac{L}{2}\) - 10) = 5 x (\(\frac{L}{2}\) - 15)
\(\frac{3L}{2}\) - 30) = \(\frac{5L}{2}\) - 75)
\(\frac{5L}{2}\) - \(\frac{3L}{2}\) = 75 - 30 = 45
L = \(\frac{2L}{2}\) = 45 cm
From equation (ii) 400 x 6 = m x (\(\frac{L}{2}\) - 15)
2400 = m x (\(\frac{45}{2}\) - 15)
2400 = m x 7.5
m = \(\frac{2400}{7.5}\) = 320 g
Therefore, I. m = 320g and II. L = 45 cm
(d) Reasons for less pressure at the top of a mountain:
The lower pressure at the top of a mountain is due to the reduced number of air molecules in the atmosphere above that elevation, resulting in a lighter air column and fewer molecular collisions, which together create lower atmospheric pressure compared to sea level.
(e)(i) Density = \(\rho\) = \(\frac{m}{v}\)
m = v x \(\rho\), but v = A x h
m = A x h x \(\rho\) = 13.6 x 10\(^3\) x 40 x 20 x 10\(^{-6}\) = 10.88kg
(e)(ii) pressure exerted by the surface of the mercury
P\(_t\) = P\(_{atm}\) + pressure of mercury
P\(_{atm}\) = P\(_t\) - \(\rho\) x h x g = 1.42 x 10\(^5\) - 13.6 x 10\(^3\) x 0.2 x 10 = 1.148 x 10\(^5\)Pa
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}