ai. State the reason why simple harmonic motion is periodic.
ii. State two factors that affect the period of oscillation of a simple pendulum.
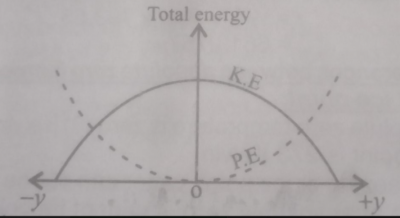
iii. Sketch a graph of the total mechanical energy, E, against displacement, y, for the motion of a simple pendulum from one extreme position to the other.
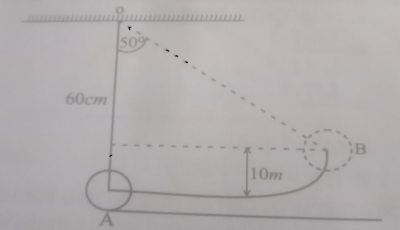
b. The diagram above illustrates an oscillatory pendulum. Calculate the work done in raising the pendulum to point B, if the mass of the bob is 50 g.
[g = \(10 ms^2\)] see the figure above
c. A spiral spring of spring constant, k, and natural length, l, has a scale pan of mass 0.04 kg hanging on its lower end while the upper end is firmly fixed to a support. When an object of mass 0.20 kg is placed on the scale pan, the length of the spring becomes 0.055 m and when the object is replaced with another object of mass 0.28 kg, the length of the spring becomes 0.065 m. Calculate the values of k and l.
[g = \(10 ms^2\)]
ai. Simple harmonic motion is periodic because of the restoring force which is proportional to the displacement, acts in the opposite direction to the motion
ii. ♦ Length of the pendulum ♦ Strength of the gravitational field
iii. See the figure above.
b. m = 50g = 0.05kg, g = 10 \(ms^2\), h = 10cm = 0.1m, P.E = ?
P.E = mgh = 0.05 × 10 × 0.1
∴ P.E = 0.05 J
c. Let the extension be ∆l
F = k ∆l = k(\(l_n\) - l )
where k is the spring constant, ln is the new length, l is the natural length, and F = mg.
Total mass = mass of pan + added mass
In the first case,
\(m_1\) = 0.04 + 0.20 = 0.24 kg
\(F_1\) = 0.24 × 10 = 2.4 N
∆l = 0.055 - l
Since F = k ∆l,
2.4 = k(0.055 - l )
2.4 = 0.055k - l k --- (i)
In the second case,
\(m_2\) = 0.04 + 0.28 = 0.32 kg
\(F_2\) = 0.32 × 10 = 3.2 N
∆l = 0.065 - l
Since F = k ∆l,
3.2 = k(0.065 - l )
3.2 = 0.065k - l k --- (ii)
Subtracting equation (i) from (ii)
⇒ 0.8 = 0.01k
k = \(\frac{0.8}{ 0.01}\)
Substitute (80) for k in equation (i)
⇒ 2.4 = 0.055(80) - 80 l
⇒ 2.4 = 4.4 - 80 l
⇒ 80 l = 4.4 - 2.4
⇒ 80 l = 2
l = \(\frac{2}{80}\)
Therefore, the value of k = 80 N/m and l = 0.025 m
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}