(a) Explain what is meant by: (i) electric field intensity ; (ii) electric lines of force.
(b) Two similar but opposite point charges -q and +q each of magnitude \(5 \times 10^{-8} C\) are seperated by a distance of 8.0cm in vacuum as shown in the diagram below.

Calculate the magnitude and direction of the resultant electric field intensity E at the point P. Draw the lines of force due to this system of charges. [Take \(\frac{1}{4 \pi \varepsilon _{0}}\)]
(c) 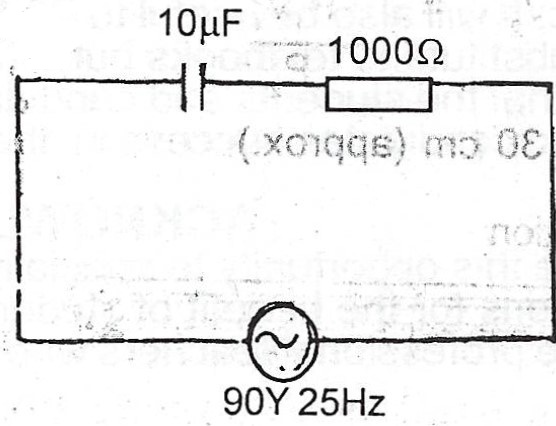
Calculate the following in the series circuit shown above: (i) reactance of the capacitor ; (ii) impedance of the circuit ; (iii) current through the circuit ; (iv) voltage across the capacitor ; (v) average power used in the circuit.
(a)(i) Electric Field Intensity: An electric field is a region in which a force of electrical origin is experienced. Electric Field Intensity (E) at any point is the force per unit charge which the field exerts at that point. The S.I unit is NC\(^{-1}\). It is a vector quantity and its direction is the same as that of the force or a small positive test charge placed in the field. Mathematically,
\(E = \frac{F}{q}\), F - force and q - charge.
(ii) Electric Lines of Force: Electric lines of force are imaginary lines used to represent electric field patterns. They have the following characteristics:
(1) At any point, the tangent to a line of force gives the direction of E at that point.
(2) The number of lines per unit cross-sectional area is proportional to the magnitude of electric field. The closer the lines, the larger the electric field.
(b) 
Field due to -q at p:
\(E_{1} = \frac{q}{4 \pi \varepsilon _{0} r^{2}}\)
= \(\frac{-5.0 \times 10^{-8}}{0.05^{2}} \times 9 \times 10^{9}\)
= \(- 180000 NC^{-1}\)
\(E_{2} = \frac{+ q}{4 \pi \varepsilon _{0} r^{2}}\)
= \(\frac{5.0 \times 10^{-8}}{0.03^{2}} \times 9 \times 10^{9}\)
= \(+ 500000 NC^{-1}\)
\(\therefore\) Resultant of the electric field intensity E at the point P is
\(E = E_{1} + E_{2} = 500000 - 180000 = 320000 NC^{-1}\)
In the direction of the positive charge.
(c) 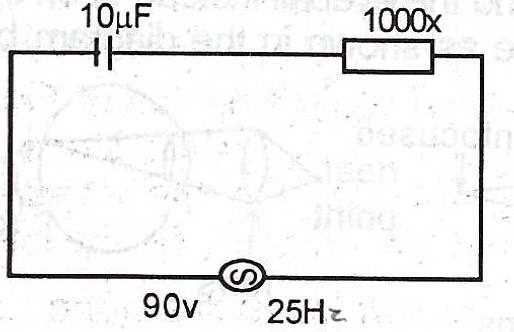
(i) Reactance of the capacitor \(X_{c} = \frac{1}{\omega c} = \frac{1}{2 \pi f c}\)
= \(\frac{1}{2 \times \pi \times 25 \times 10 \times 10^{-6}} = \frac{2000}{\pi} \Omega\)
(ii) Impedance of the circuit, \(Z = \sqrt{X_{c} ^{2} + R^{2}}\)
= \(\sqrt{(\frac{2000}{\pi})^{2} + 1000^{2}}\)
= \(\sqrt{(636.62)^{2} + (1000)^{2}}\)
= \(\sqrt{1405285.0244}\)
= \(1185.45 \Omega\)
(iii) Current through the circuit, \(I = \frac{E}{Z}\)
= \(\frac{90}{1185.45} = 0.0759 A_{rms}\)
(iv) Voltage across the capacitor \(V = IX_{c}\)
= \(0.0759 \times 636.62\)
= \(48.319 V_{rms}\)
(v) Average power used in the circuit \(P = IV\)
= \(I^{2} Z\)
= \((0.0759)^{2} \times 1185.45\)
= \(6.829 W\)
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}