A frustrum of pyramid with square base has its upper and lower sections as squares of sizes 2m and 5m respectively and the distance between them 6m. Find the height of the pyramid from which the frustrum was obtained.
The lateral view of the frustrum
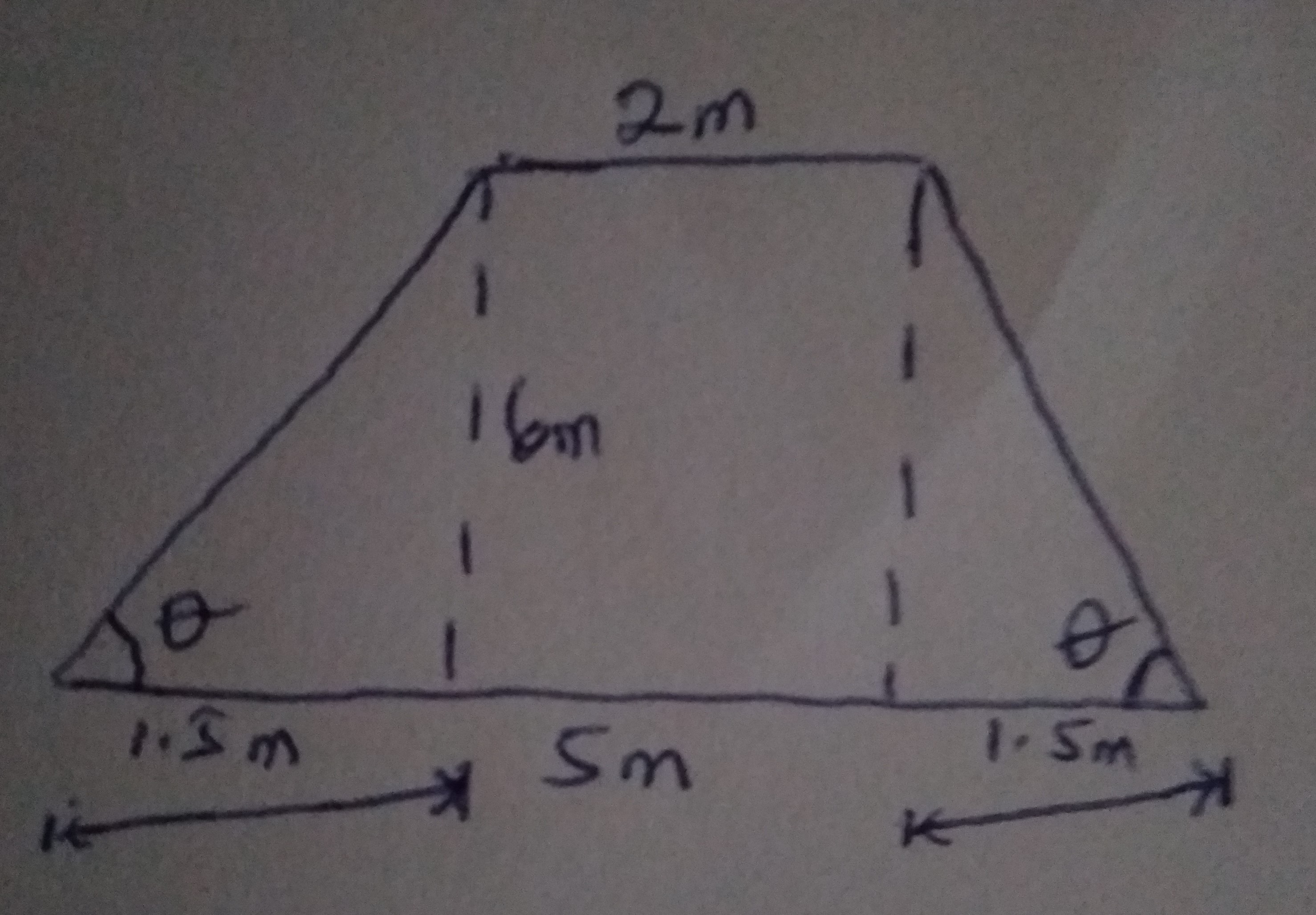
\(\tan \theta = \frac{6}{1.5} = 4\)
\(\theta = \tan^{-1} 4 = 75.96°\)
Extending to the full height of the pyramid, we have
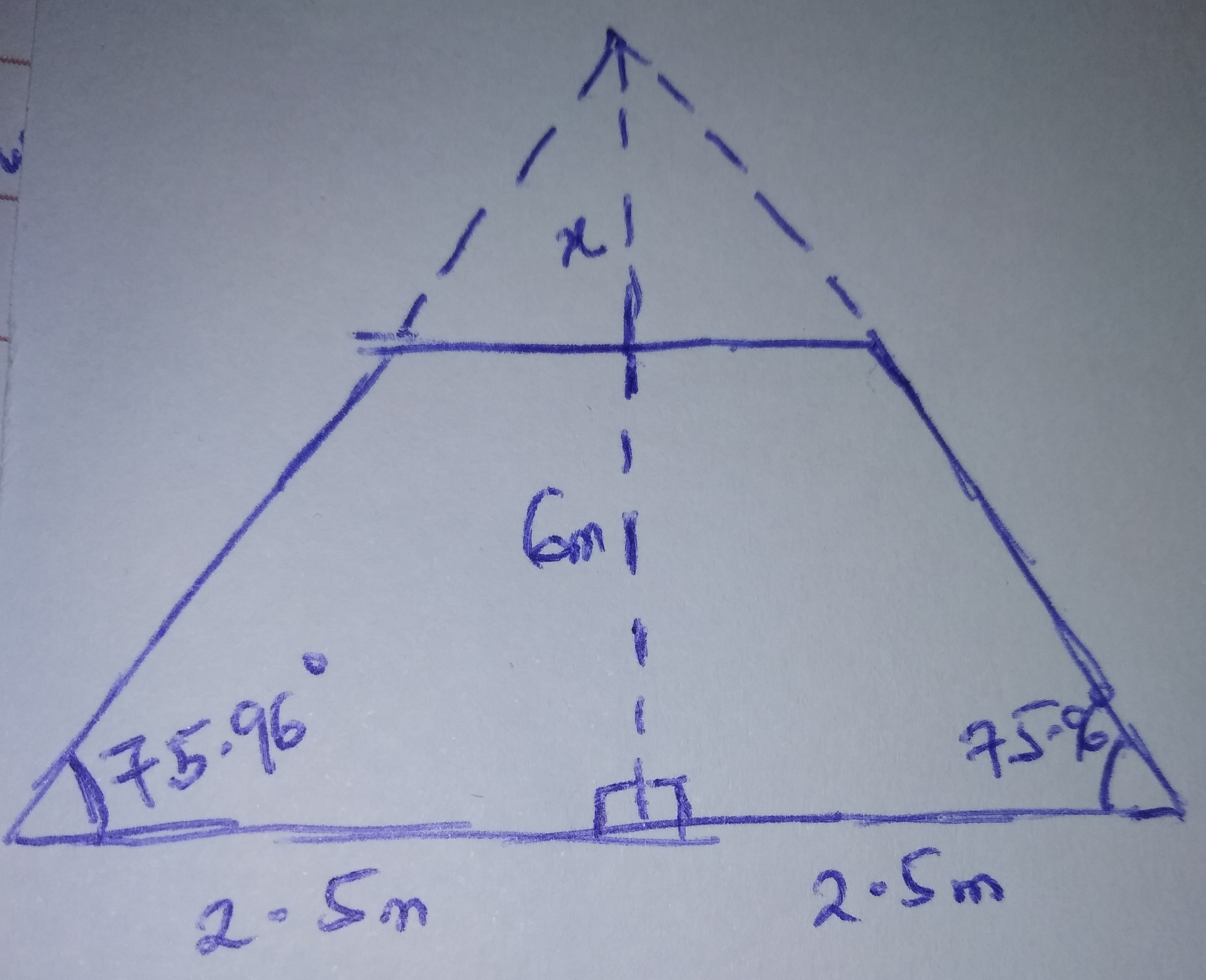
The height of the pyramid which formed the frustrum = (6 + x)m,
\(\tan 75.96 = \frac{6 + x}{2.5}\)
\(6 + x = 2.5 \times 4 = 10.0\)
\(\therefore \text{The height of the pyramid} = 10.0m\)
There is an explanation video available below.
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}