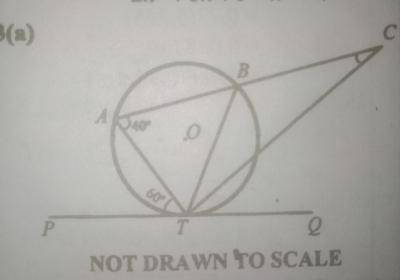
(a) In the diagram above, ABT is a circle centre O. \(\overline{PQ}\) is a tangent to the circle at T and ABC is a straight line. \(\overline{TC}\) bisects \(\angle\)BTQ, \(\angle\)BAT = 44º and \(\angle\)PTA = 60º. Find \(\angle\)ACT
(b) The circumference of the base of a cylindrical tank is 11 m. The height of the tank is 3 m more than 6 times the base radius. Calculate the:
(i) radius; (ii) height; (iii) volume of the tank.
(a) \(\frac{B\widehat{T}Q}{2}\) = B\(\widehat{T}\)C = C\(\widehat{T}\)Q (\(\overline{TC}\) bisects \(\angle\)BTQ)
B\(\widehat{T}\)Q = B\(\widehat{A}\)T = 44º(angles in alternate segments)
B\(\widehat{T}\)C = \(\frac{∠BTQ}{2}\) = \(\frac{44}{2}\) = 22º
A\(\widehat{B}\)T = P\(\widehat{T}\)A = 60º (angles in alternate segments)
Now,
A\(\widehat{C}\)T + B\(\widehat{T}\)C = A\(\widehat{B}\)T (sum of opp. interior angles is equal to the exterior angle of a triangle)
A\(\widehat{C}\)T + 22º = 60º
A\(\widehat{C}\)T = 60 - 22 = 38º
(b) (i) Given: Circumference of base, 2\(\pi\)r = 11 -- - - - - - - - - - -(i)
Also, height, h = 6r + 3 - - - - - - - - - -(ii)
From, eqn (i), 2\(\pi\)r = 11, r = \(\frac{11}{2\pi}\) = 1.75 m
(ii) From equation (ii); height, h = 6r + 3 = 6(1.75) + 3 = 13.5 m
(iii) Volume of cylinder, V = \(\pi r^2\)h = \(\frac{22}{7} \times 1.75^2\) x 13.5 = 130 m\(^3\)
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}