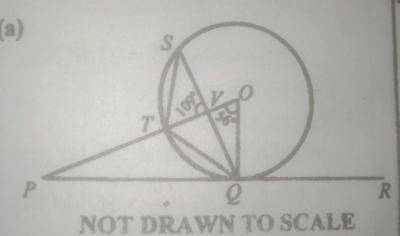
(a) In the diagram above, \(\overline{PR}\) is a tangent to the circle O at Q. \(\angle\)POQ = 56º and \(\overline{PO}\) intersect \(\overline{SO}\) at V such that \(\angle\)SVP = 109º. Calculate: (i) \(\angle\)TQP (ii) \(\angle\)QTS
(b) Simplify \(\frac{2n^2 - 3n - 2 }{2n^2 + 3n + 1} \times \frac{n^2 - 1}{n^2 - 4}\)
(i) 2 x T\(\widehat{S}\)Q = P\(\widehat{O}\)Q (2 times angle at circumference = angle at centre of circle)
T\(\widehat{S}\)Q = \(\frac{P\widehat{O}Q}{2}\) = \(\frac{56}{28}\) = 28º
T\(\widehat{Q}\)P = T\(\widehat{S}\)Q (angles in alternate segment}
(ii) S\(\widehat{T}\)O + T\(\widehat{S}\)Q + S\(\widehat{V}\)P = 180º (sum of angles in a \(\triangle\))
S\(\widehat{T}\)O + 28º + 109º = 180º
S\(\widehat{T}\)O = 180º - 28º - 109º = 43º
Now,
O\(\widehat{T}\)Q = O\(\widehat{Q}\)T (base angles of an isosceles triangle)
O\(\widehat{T}\)Q + O\(\widehat{Q}\)T + P\(\widehat{O}\)Q = 180º
2(O\(\widehat{T}\)Q) = 180 - 56 = 124º
O\(\widehat{T}\)Q = \(\frac{124}{2}\) = 62º
Q\(\widehat{T}\)S = S\(\widehat{T}\)O + O\(\widehat{T}\)Q = 42 + 62 = 105º
(b) \(\frac{2n^2 - 3n - 2 }{2n^2 + 3n + 1} \times \frac{n^2 - 1}{n^2 - 4}\)
= \(\frac{(2n + 1)(n - 2)}{(2n + 1)(n + 1)} \times \frac{(n + 1)(n - 1)}{(n + 2)(n - 2)}\)
After canceling common factors
= \(\frac{n - 1}{n + 2}\)
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}