The diameter of a circle centre O is 26 cm. If a chord \(\overline{PQ}\) is drawn such that it is 5 cm from O to the centre of the chord, calculate, correct to the nearest whole number, the
(a)\(\angle\)POQ
(b) Area of the minor segment formed by the chord \(\overline{PQ}\). [take \(\pi\) = \(\frac{22}{7}\)]
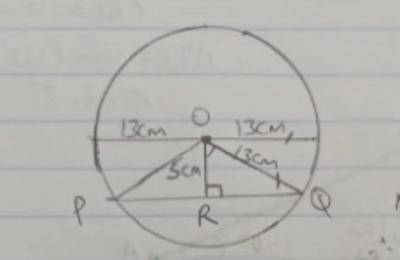
Given diameter d = 20cm
radius r = \(\frac{20}{2}\) = 10cm
\(\overline{OQ}\) = radius
NOTE: \(\overline{OR}\) bisects \(\overline{PQ}\) and \(\triangle\)POQ, \(\overline{PR}\) = \(\overline{RQ}\)
Cos(Q\(\widehat{O}\)R) = \(\frac{5}{13}\)
(Q\(\widehat{O}\)R) = cos\(^{-1}\)((\(\frac{5}{13}\)) = 67.38º
P\(\widehat{O}\)R = 2 x Q\(\widehat{O}\)R = 2 x 67.38 = 134.76 ≈ 135( nearest whole number)
(b) Area of minor segment = Area of minor sector P\(\widehat{O}\)Q - Area of triangle P\(\widehat{O}\)Q
= [\(\frac{P\widehat{O}Q}{360}\) x \(\pi\) x |OQ|\(^2\)] - [\(\frac{1}{2}\) x |OQ|\(^2\) x sin(P\(\widehat{O}\)Q)]
= [\(\frac{135}{360}\) x \(\frac{22}{7}\) x 13\(^2\)] - [\(\frac{1}{2}\) x 13\(^2\) x Sin(134.76)]
= 198.745 - 60 = 138.745 = 139cm\(^2\) (to the nearest whole number)
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}