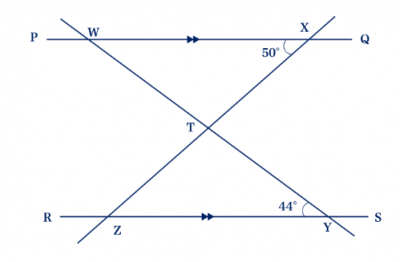
In the diagram above, \(\overline{PQ}\) || \(\overline{RS}\), \(\angle\)WYZ = 44º and \(\angle\)WXY = 50º. Find \(\angle\)WTX
\(\angle\)XWY = \(\angle\)ZYW = 44º (alternate \(\angle\)s)
Considering \(\triangle\)WTX
\(\angle\)W + \(\angle\)T + \(\angle\)X = 180º
44 + \(\angle\)T + 50 = 180
\(\angle\)T = 180 - 44 - 50 = 86º
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}