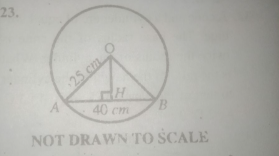
In the diagram above, O is the centre of the circle. If | \(\overline{OA}\) = 25 cm and |\(\overline{AB}\) = 40 cm, find |\(\overline{OH}\)|
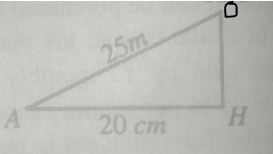
Line OH divides Line AB into two halves, therefore, Line AH = Line HB = 20cm
Considering \(\triangle\) AOH
(\(\overline{OH})^2\) = 25\(^2\) - 20\(^2\) = 625 - 400 = 225
Taking the square root of both sides
(\(\overline{OH}\) = \(\sqrt{225}\) = 15 cm
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}