(a) Copy and complete the table of values for the relation y=2x\(^2\) - x - 2 for 4 ≤ x ≤ 4.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 19 | -2 | 26 |
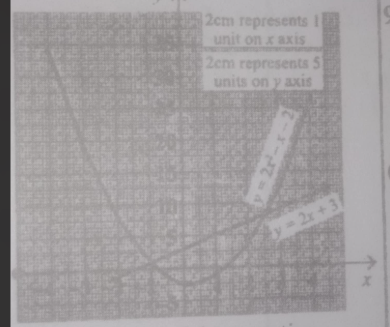
(b) Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of y = 2x\(^2\) - x - 2 for 4 ≤ x ≤ 4.
(c) On the same axes, draw the graph of y = 2x + 3.
(d) Use the graph to find the: (i) roots of the equation 2x-3r-5 0; (i) range of values of x for which 2x\(^2\) -x - 2<0.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 34 | 19 | 8 | 1 | -2 | -1 | 4 | 13 | 26 |
SEE THE GRAPH ABOVE
(c) Straight line graph of y = 2x + 3
(d) The roots of 2x\(^2\) -3x - 5 = 0 are x=-1 ± 0.1 or 2.5 ± 0.1
(ii) The range of values of x for which -x -2 < 0is (-0.7± 0.1) < x < (1.3 ± 0.1)
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}