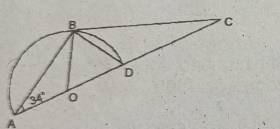
In the diagram, \(\overline{AD}\) is a diameter of a circle with Centre O. If ABD is a triangle in a semi-circle ∠OAB=34",
find: (a) ∠OAB (b) ∠OCB
∠OAB = ∠OBA=34°
∠ABD = 90
∠OBD = ∠ABD - ∠0BA = 90 - 34 = 56
From triangle OBC
∠BOC + ∠OBC + ∠OCB = 180°
∠BOD = ∠2OAB = 68°
= 68° + 90° + ∠0CB = 180
∠OCB = 180 - 158 = 22
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}