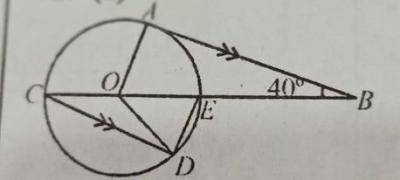
(a) In the diagram, AB is a tangent to the circle with centre O, and COB is a straight line. If CD//AB and < ABE = 40°, find: < ODE.
(b) ABCD is a parallelogram in which |\(\overline{CD}\)| = 7 cm, I\(\overline{AD}\)I = 5 cm and < ADC= 125°.
(i) Illustrate the information in a diagram.
(ii) Find, correct to one decimal place, the area of the parallelogram.
(c) If x = \(\frac{1}{2}\)(1 - \(\sqrt{2}\)). Evaluate (2x\(^2\) - 2x).
< AOB = 108\(^o\) - (90\(^o\) + 40\(^o\))
= 180\(^o\) - 130\(^o\) = 50\(^o\)
< DCO = 40\(^o\) (Alternate angle)
< ODE = \(\frac{180^o - 80^o}{2}\) = \(\frac{100^o}{2}\)
= 50\(^o\)
(b)(i)

(b)(ii) Area of the parallelogram
= ab sin \(\theta\)
= 5cm x 7cm sin 125\(^3\)
= 35 sin 125
= 28.7cm\(^2\)
(c)
x = \(\frac{1}{2}(1 - \sqrt{2})\)
evaluate (2x\(^2\) - 2x)
= 2[\(\frac{1}{2}(1 - \sqrt{2})^2\)] - 2[\(\frac{1}{2} (1 - \sqrt{2}\))]
= 2[\(\frac{1}{4}(1 - 2\sqrt{2} + 2)\)] - 1 + \(\sqrt{2}\)
= 2[\(\frac{1}{4}(3 - 2\sqrt{2})\) - 1 + \(\sqrt{2}\)]
2[\(\frac{3}{4} - \frac{1}{2} \sqrt{2} - 1 + \sqrt{2}\)]
= \(\frac{3}{2} - \sqrt{2} - 2 + 2\sqrt{2}\)
= \(\frac{1}{2} + \sqrt{2}\)
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}