PART II
A particle of weight 12 N lying on a horizontal ground is acted by forces F\(_1\) = (10 N, 090º), F\(_2\) = (16 N, 180º), F\(_3\) = (7 N, 300º) and F\(_4\) = (12N, 030º)
(a) Express all the forces acting on the particle as column vectors
(b) Find, correct to two decimal places, the magnitude of the:
(i) resultant forces;
(ii) acceleration with which the particle starts to move.[Take g = 10 ms\(^{-2}\)]
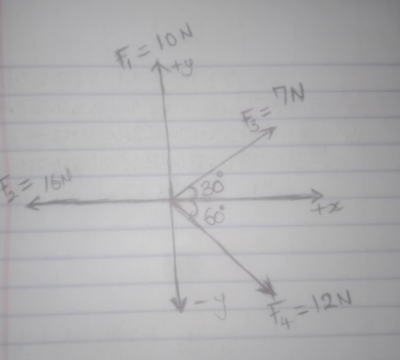
W = 12 N
From the diagram above,
| F(N) | F\(_x\) | F\(_y\) |
| 10 | 10cos90 | 10sin90 |
| 16 | 16cos180 | 16sin180 |
| 7 | 7cos30 | 7sin30 |
| 12 | 12cos300 | 12sin300 |
\(\sum{F_x}\) = - 3.938 N, \(\sum{F_y}\) = 3.108 N
Expressing in column vector
\(\begin{pmatrix} i & j \\ 10cos 90º & 10sin90º \\ 16cos180º & 16sin180º \\ 7cos30º & 7sin30º \\ 12cos 300º & 12sin300º \end{pmatrix}\)
Resultant R = \(\sqrt{(F_x)^2 + (F_y)^2}\)
R = \(\sqrt{( - 3.938)^2 + (3.108)^2}\) = 5.018N ≈ 5.02 N
(ii) R = ma (from Newton's law)
But, W = mg
m = \(\frac{\text{W}}{\text{g}}\) = \(\frac{12}{10}\) = 1.2 kg
From, R = ma, then, a = \(\frac{\text{R}}{\text{m}}\) = \(\frac{5.018}{1.2}\) = 4.182ms\(^{-2}\) ≈ 4.18 ms\(^{-2}\)
Contributions ({{ comment_count }})
Please wait...
Modal title
Report
Block User
{{ feedback_modal_data.title }}