Explanation

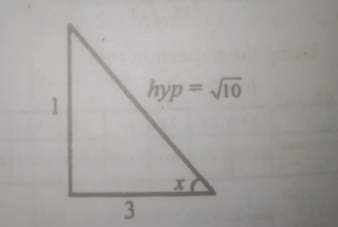
hyp\(^2\) = 3\(^2\) + 1\(^2\) (Pythagoras's theorem)

hyp = \(\sqrt{10}\)

Given: tan x =  \(\frac{1}{3}\) ( sin and cos will be in the third quadrant and are both negative where 180º < x < 270º)

sin x =  \(\frac{-1}{\sqrt{10}}\), cos x = \(\frac{-3}{\sqrt{10}}\)

\(\frac{sin2 x - cos x}{2 tan x + sin 2x}\) =  \(\frac{2sinx cos x - cos x}{2 tan x + 2sin x cos x}\) but 2snx cox = \(\frac{3}{5}\)

\(\frac{sin2 x - cos x}{2 tan x + sin 2x}\) = \(\frac{\frac{3}{5} + \frac{3}{\sqrt{10}}}{2(\frac{1}{3}) + \frac{3}{5}}\) = \(\frac{\frac{3}{5} + \frac{3}{\sqrt{10}}}{\frac{19}{15}}\)

= (\(\frac{3}{5}\) + \(\frac{3\sqrt{10}}{10}\)) \(\div\) \(\frac{19}{15}\) = \(\frac{15}{19}\)[\(\frac{3}{5}\) + \(\frac{3}{\sqrt{10}}\)]

= \(\frac{9}{19}\) + \(\frac{45}{19\sqrt{10}}\)

= \(\frac{9}{19}\) + \(\frac{45 \sqrt{10}}{19(10)}\)

= \(\frac{9}{19}\) + \(\frac{9 \sqrt{10}}{19(2)}\)

= \(\frac{9}{19}\)[1 + \(\frac{\sqrt{10}}{2}\)]

• An accurate identification of a rapist can be carried out by it conducting a? Answer this

  5 Answers   ·   Chemistry   ·   1 day ago
• please, who's good at chemistry (specifically: Stoichiometry and other topics) pls help a sister in need🙏? Answer this

  3 Answers   ·   Chemistry   ·   3 hours ago
• Can I get the formulas for the topic of work function? Answer this

  0 Answers   ·   Physics   ·   1 hour ago