(a) Using ruler and a pair of compasses only, construct :

(i) a quadrilateral PQRS such that /PQ/ = 7 cm, < QPS = 60°, /PS/ = 6.5 cm, < PQR = 135° and /QS/ = /QR/ ;

(ii) locus, \(l_{1}\) of points equidistant from P and Q ;

(iii) locus, \(l_{2}\) of points equidistant from P and S.

(b)(i) Label the point T where \(l_{1}\) and \(l_{2}\) intersect. (ii) With center T and radius /TP/, construct a circle \(l_{3}\).

(a)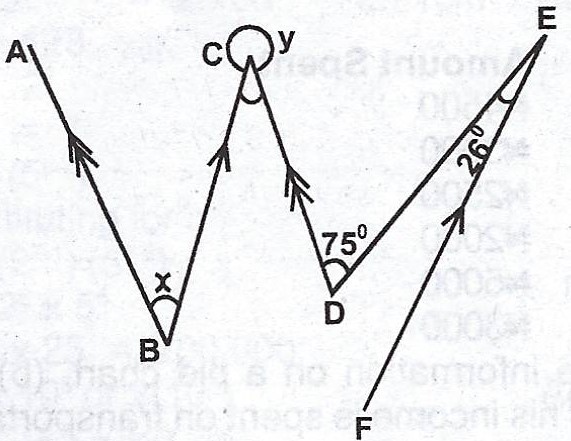 

In the diagram, AB // CD and BC // FE. \(\stackrel\frown{CDE} = 75°\) and \(\stackrel\frown{DEF} = 26°\). Find the angles marked x and y.

(b)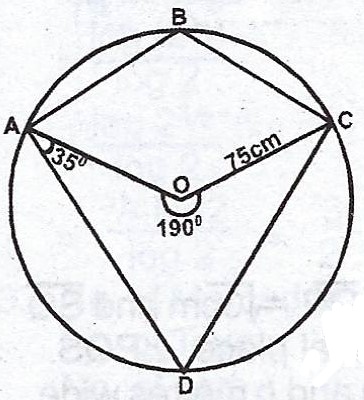 

The diagram shows a circle ABCD with centre O and radius 7 cm. The reflex angle AOC = 190° and < DAO = 35°. Find :

(i) < ABC ; (ii) < ADC.

(c) Using the diagram in (b) above, calculate, correct to 3 significant figures, the length of : (i) arc ABC ; (ii) the chord AD. [Take \(\pi = 3.142\)].

(a) Copy and complete the table of values for \(y = 3\sin x + 2\cos x\) for \(0° \leq x \leq 360°\).

(b) Using a scale of 2 cm to 60° on x- axis and 2 cm to 1 unit on the y- axis, draw the graph of \(y = 3 \sin x + 2 \cos x\) for \(0° \leq x \leq 360°\).

(c) Use your graph to solve the equation : \(3 \sin x + 2 \cos x = 1.5\).

(d) Find the range of values of x for which \(3\sin x + 2\cos x < -1\).

(a) If 3, x, y, 18 are the terms of an Arithmetic Progression (A.P), find the values of x and y.

(b)(i) The sum of the second and third terms of a grometric progression is six times the fourth term. Find the two possible values of the common ratio.

(ii) If the second term is 8 and the common ratio is positive, find the first six terms.

(a) Evaluate, without using mathematical tables or calculator, \((3.69 \times 10^{5}) \div (1.64 \times 10^{-3})\), leaving your answer in standard form.

(b) A man invested N20,000 in bank A and N25,000 in bank B at the beginning of the year. Bank A pays simple interest at a rate of y% per annum and B pays 1.5y% per annum. If his total interest at the end of the year from the two banks was N4,600, find the value of y.