(a) How many numbers between 75 and 500 are divisible by 7?
(b) The 8th term of an Arithmetic Progression (A.P) is 5 times the 3rd term while the 7th term is 9 greater than the 4th term. Write the first 5 terms of the A.P.
(a) Without using calculator or tables, find the value of \(\log 3.6\) given that \(\log 2 = 0.3010, \log 3 = 0.4771\) and \(\log 5 = 0.6990\).
(b) If all numbers in the equation \(\frac{y}{y + 101} = \frac{11}{10010}\) are in base two, solve for y.
(a) Solve the inequality : \(\frac{2}{5}(x - 2) - \frac{1}{6}(x + 5) \leq 0\).
(b) Given that P = \(\frac{x^{2} - y^{2}}{x^{2} + xy}\),
(i) express P in its simplest form ; (ii) find the value of P if x = -4 and y = -6.
The table below shows how a man spends his income in a month.
| Items | Amount Spent |
| Food | N4500 |
| House Rent | N3000 |
| Provisions | N2500 |
| Electricity | N2000 |
| Transportation | N5000 |
| Others | N3000 |
(a) Represent the information on a pie chart.
(b) What percentage of his income is spent on transportation?
(a) A pentagon is such that one of its exterior sides is 60°. Two others are (90 - m)° each while the remaining angles are (30 + 2m)° each. Find the value of m.
(b) 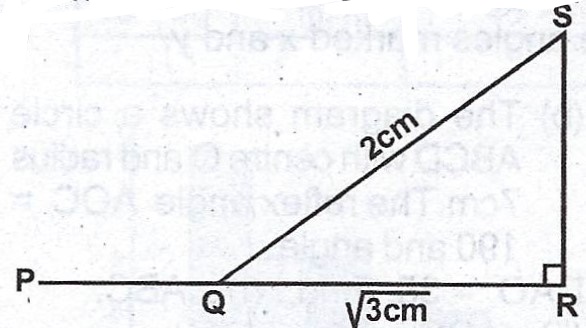
In the diagram, PQR is a straight line, \(\overline{QR} = \sqrt{3} cm\) and \(\overline{SQ} = 2 cm\). Calculate, correct to one decimal place, < PQS.